How To Add Fractions With Lcm

Calculation Fractions With Unlike Denominators

Calculation fractions with unlike denominators ways nosotros need to add fractions that have different denominators. In this case, we catechumen the given fractions to similar fractions to go common denominators so that information technology becomes easier to add them. This is done by finding the Least Common Multiple (LCM) of the given denominators. Nosotros catechumen each fraction in such a manner and then that nosotros have a common denominator, and so we add the numerators to get the sum.

In this article, we volition learn how to add fractions with different denominators stepwise. We volition also discuss the addition of mixed fractions with unlike denominators along with a few solved examples for a improve understanding of the concept.

one.	What is Adding Fractions with Unlike Denominators?
2.	Steps For Adding Fractions with Dissimilar Denominators
three.	How to Add Fractions with Dissimilar Denominators?
4.	Adding Mixed Numbers with Unlike Denominators
5.	FAQs on Adding Fractions with Unlike Denominators

What is Calculation Fractions with Unlike Denominators?

When the denominators are non the aforementioned, the fractions are known as dissimilar fractions. For example, 3/5 and 6/7 are called unlike fractions considering they accept different denominators. To add 2 or more than given fractions, whose denominators are different or different, we demand to discover the Least Mutual Multiple (LCM) of the denominators. After finding the LCM, nosotros multiply the given fractions with such a number and then that their denominators remain common. After making the denominators equal, we can simply add together the numerators.

Steps For Adding Fractions with Unlike Denominators

The post-obit steps show the procedure for calculation fractions with unlike denominators.

Step i: Beginning, nosotros detect out the Least Mutual Multiple (LCM) of the given denominators.
Step 2: Then, we write down each fraction in a form such that the LCM becomes the common denominator. For this, nosotros multiply the numerator and denominator with a mutual number with the help of the LCM.
Step 3: Subsequently this pace, we add the numerators of these like fractions (which have common denominators now).
Step iv: Finally, we reduce the resultant fraction to its lowest terms, if needed.

These steps tin can exist understood with the help of the example given in the following section.

How to Add Fractions with Different Denominators?

At present, let us learn how to add fractions with unlike denominators by following the steps given above.

Example: Add 5/six + 7/3

Solution:

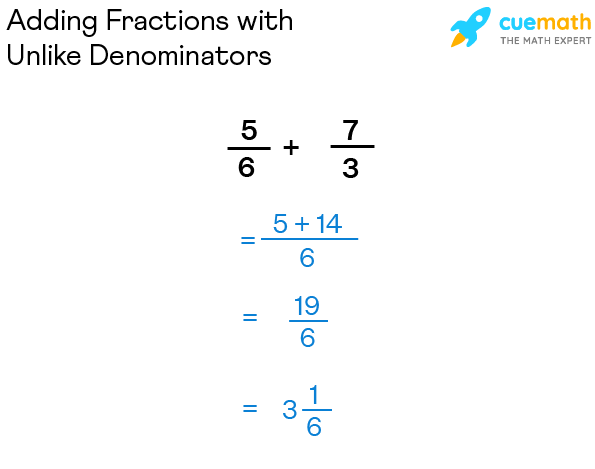
Adding Fractions with Unlike Denominators

Stride one: Since the fractions take different denominators, we find the LCM of half-dozen and 3. The LCM of six and 3 is half-dozen.
Step ii: Now, convert the given fractions to equivalent fractions such that the LCM becomes their common denominator. As we can come across five/6 already has the LCM as its denominator, and then we will only change the fraction 7/3 and brand information technology an equivalent fraction, which will be 14/6.
Stride three: Afterwards this, nosotros tin can add the numerators of both the fractions since the denominators are the aforementioned.
Footstep iv: 5/six + 14/half dozen = (5 + xiv)/6 = 19/6. This can be converted to a mixed fraction and written as \(three\dfrac{1}{6}\)

Calculation iii Fractions with Different Denominators

For adding three or more fractions with unlike denominators we use the same steps as given in a higher place. Let us learn how to add 3 fractions with different denominators with the help of the following example.

Case: Add together 1/2 + 3/five + 7/3

Adding 3 Fractions with DIfferent Denominators

Stride 1: First, we will find the LCM of 2, five, and iii, which is 30.
Pace 2: At present, we will make each fraction an equivalent fraction in such a manner that the LCM xxx becomes the denominator of each fraction.
Pace 3: The equivalent fractions with denominator 30 are 15/xxx, 18/30, and 70/thirty.
Pace 4: Add all the numerators (xv + 18 + 70)/thirty = 103/30. This tin be converted to a mixed fraction and written as \(three\dfrac{thirteen}{30}\)

Adding Mixed Numbers with Dissimilar Denominators

If we demand to add mixed numbers with unlike denominators, we convert the mixed fraction to an improper fraction. Later on this, we can add together the fractions past following the steps given above. Allow united states understand this with the assistance of the following example.

Instance: Add together \(5\dfrac{1}{7}\) and \(four\dfrac{1}{five}\)

Start, convert the mixed number into an improper fraction.

\(v\dfrac{1}{seven}\) = 36/seven

\(four\dfrac{one}{v}\) = 21/five

Now add 36/7 and 21/5

LCM of 7 and v is 35

Equivalent fractions

36/7 = 180/35

21/v = 147/35

At present add the numerators,

(180 + 147)/35 = 327/35 = \(ix\dfrac{12}{35}\)

Of import Notes on Calculation Fractions with Unlike Denominators

For adding fractions with unlike denominators, we take the LCM of the dissimilar denominators and convert them to like fractions and and then add the numerators.
For adding mixed fractions with unlike denominators, we convert them into improper fractions and and so add.

☛ Related Manufactures

Adding Fractions with Unlike Denominators Worksheets
Improver and Subtraction of Fractions
Subtracting Fractions with Unlike Denominators
Calculation Mixed Fractions

Adding Fractions with Unlike Denominators Examples

Example 1: Add 8/9 + 1/3 + 7/half dozen

Solution: For adding fractions with different denominators, first, we will discover out the LCM of numbers nine, 3 and 6

LCM = 18

Now, we will convert each fraction into equivalent fractions by taking the denominator every bit the LCM

8/9 = 16/18

1/iii = half dozen/18

7/vi = 21/18

Now, we tin can add together the numerators.

(16 + half dozen + 21)/xviii = 43/18. This tin be converted to a mixed fraction \(2\dfrac{seven}{18}\)
Example 2: Add 5/8 + 1/5

Solution: To add fractions with unlike denominators, first, we will discover out the LCM of numbers eight and five

LCM = 40

And then, nosotros will catechumen each fraction into equivalent fractions past taking the denominator as the LCM 40

5/eight = 25/xl

ane/5 = 8/40

At present, we can add the numerators.

(25 + eight)/40 = 33/40

So, the sum of v/8 + ane/five is 33/xl
Example three: Add mixed fractions \(3\dfrac{i}{4}\) and \(2\dfrac{2}{3}\)

Solution: To add together the given mixed fractions, we start convert them into improper fractions.

\(three\dfrac{ane}{4}\) = 13/iv and \(2\dfrac{2}{3}\) = eight/3

Now, since the denominators are dissimilar, we have the LCM of 3 and four. LCM (three, 4) = 12. Now, convert the fractions into like fractions.

thirteen/iv = 39/12 and viii/three = 32/12. Now add the two fractions.

39/12 + 32/12 = 71/12 = \(5\dfrac{11}{12}\)

Answer: \(3\dfrac{1}{4}\) + \(2\dfrac{2}{3}\) = \(5\dfrac{11}{12}\)

go to slidego to slidego to slide

Breakup tough concepts through simple visuals.

Math will no longer exist a tough subject, peculiarly when you sympathize the concepts through visualizations.

Book a Free Trial Course

Adding Fractions With Unlike Denominators Questions

become to slidego to slide

FAQs on Adding Fractions with Unlike Denominators

How to Add Fractions with Different Denominators?

Adding fractions with dissimilar denominators means that two fractions that accept different denominators need to exist added. In this case, nosotros convert the given fractions to like fractions to go mutual denominators and so that it becomes easier to add them. This is done past finding the Least Common Multiple (LCM) of the given denominators. We need to convert each fraction in such a way then that nosotros take a common denominator and afterward that, we add the numerators to get the sum.

What are the Examples of Adding Fractions with Dissimilar Denominators?

An example of adding fractions with different denominators is given as follows. Let us add together 1/three + 6/5.

We can see that the denominators are not the same, hence, nosotros demand to make the denominators equal, later which we tin can add the fractions.
In this example, 1/three + 6/v, we will beginning discover the LCM of the denominators three and 5 which is 15.
And so, we will multiply both the fractions with such a number so that the denominators remain the same.
This results in (5 + 18)/xv = 23/15.
At present, let the states convert the improper fraction to a mixed number: 23/15 = \(one\dfrac{8}{xv}\)

What is the Strategy for Adding Fractions with Unlike Denominators?

The strategy for adding fractions with unlike denominators is to discover the LCM of the given denominators and make each fraction as an equivalent fraction with the LCM equally the denominator.

What are the Steps For Adding Fractions with Unlike Denominators?

The steps for calculation fractions with unlike denominators are given beneath. Allow us empathize this with an example and add 1/5 + i/10

Stride ane: First, nosotros will discover the LCM of 5 and ten which is 10.
Step 2: Now, make each fraction an equivalent fraction in such a way so that the LCM (ten) becomes the denominator of each fraction.
Step 3: The equivalent fractions with denominator x will be ii/x and one/10
Pace 4: Add together the numerator office (2 + i)/10 = 3/10

Can we Add Fractions with Different Denominators Without Using LCM?

No, we cannot add together fractions with unlike denominators without using the LCM.

What is the Rule for Calculation Fractions with Unlike Denominators?

The basic rule for adding fractions with dissimilar denominators is to detect the LCM of the dissimilar denominators and convert the given unlike fractions into like fractions. This tin be done by changing their denominators equal to the LCM. Once the denominators go the aforementioned, the numerators can be added.

How to Add iii Fractions with Different Denominators?

In guild to add 3 fractions with different denominators, we employ the same rules that are used for adding 2 fractions with different denominators. For example, let us add together ane/6 + 1/3 + 1/2

We need to observe the LCM of half dozen, iii, and two which is half-dozen. Now, nosotros volition convert each fraction into an equivalent fraction using LCM equally the denominator.

1/half dozen = one/6

1/iii = 2/6

1/2 = 3/6

At present, add the numerators of these fractions which is: 1/half dozen + ii/6 + 3/6 = (i + 2 + three)/6 = 6/6. This fraction can be further reduced to 1 after simplifying.

How to Add and Subtract Fractions with Unlike Denominators?

In order to add together and subtract fractions with different denominators, we apply the same rules. We demand to find the LCM of the dissimilar denominators and catechumen the given dissimilar fractions into like fractions. After this step, we add or subtract the numerators according to the question.

How to Add together Fractions with Whole Numbers and Different Denominators?

In guild to add fractions with whole numbers and different denominators, we should write the whole number in its fraction course, that is, write one as its denominator and and so add it using the aforementioned rules for the addition of fractions. For example, permit u.s.a. add half dozen + iii/4 + 1/two.

In this instance, 6 is the whole number and we can write it equally half-dozen/1.
And so, permit united states rewrite the fractions every bit 6/ane + 3/4 + i/two.
Then, we will notice the LCM of the denominators and then that they are converted to similar fractions. The LCM of 1, 4, and 2 will be 4.
Now, the fractions tin can be written as 6/1 + iii/iv + 1/2 = (24 + 3 + 2)/four = 29/4. This can exist converted to mixed fraction as \(7\dfrac{i}{4}\)

How to Add Improper Fractions with Different Denominators?

In order to add improper fractions with different denominators, we use the same rules that are used for the addition of fractions. For case, let us add these improper fractions with unlike denominators: vii/ii + viii/iii.

We will first detect the LCM of the denominators. The LCM of two and 3 is 6.
So, we will convert the given fractions into equivalent fractions. So, 7/2 volition get 21/6, and 8/3 will become 16/six.
Now, we can add together them because their denominators are the same. This means (21 + sixteen)/6 = 37/half-dozen = \(vi\dfrac{i}{6}\)